New paper out on Neural ODEs for structural identification

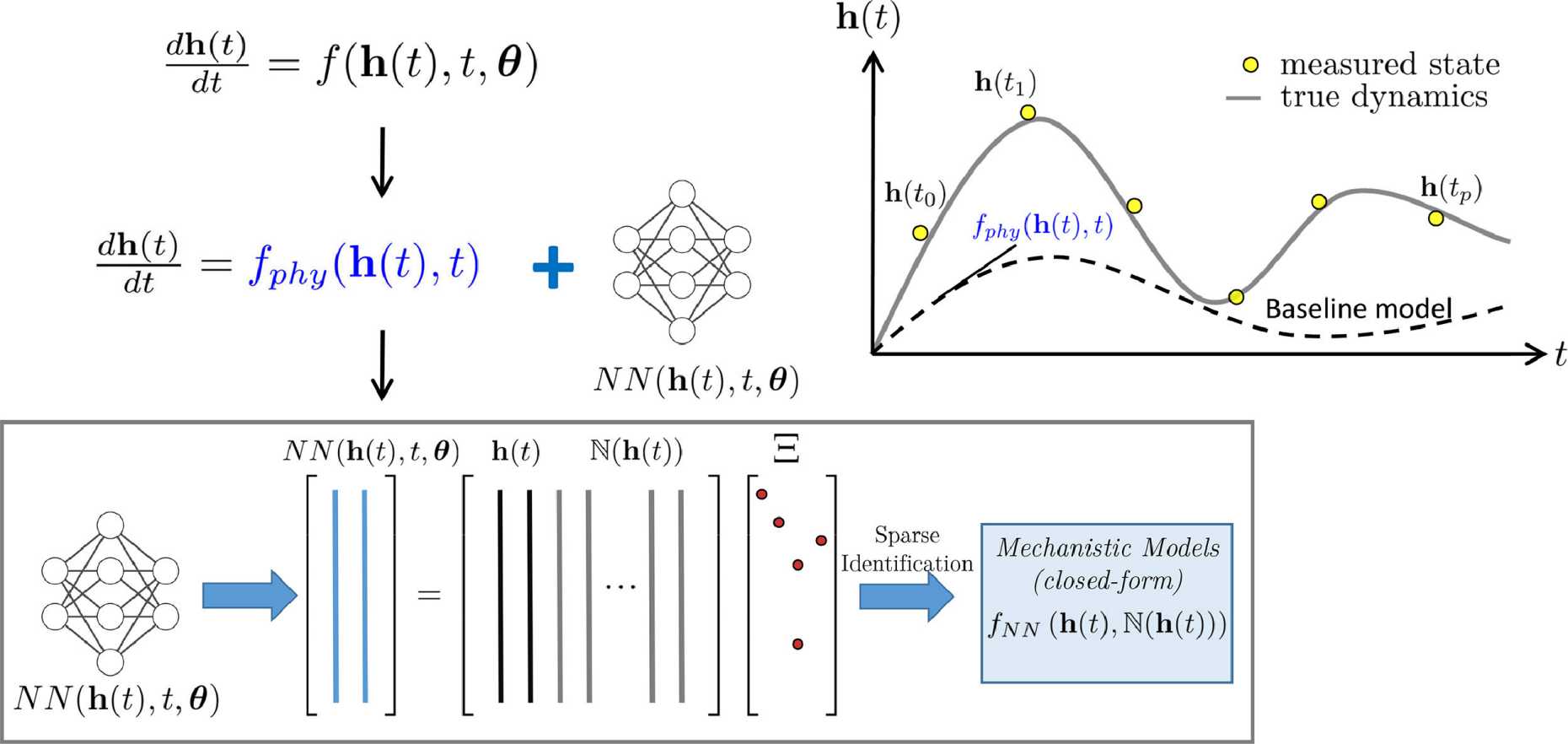
This paper exploits a new direction of structural identification by means of Neural Ordinary Differential Equations (Neural ODEs), particularly constrained by domain knowledge, such as structural dynamics, thus forming Physics-informed Neural ODEs, aiming at governing equations discovery/approximation. Structural identification problems often entail complex setups featuring high-dimensionality, or stiff ODEs, which pose difficulties in the training and learning of conventional data-driven algorithms who seek to unveil the governing dynamics of a system of interest. In this work, Neural ODEs are re-casted as a two-level representation involving a physics-informed term, that stems from possible prior knowledge of a dynamical system, and a discrepancy term, captured by means of a feed-forward neural network. The re-casted format is highly adaptive and flexible to structural monitoring problems, such as linear/nonlinear structural identification, model updating, structural damage detection, driving force identification, etc. As an added step, for inferring an explainable model, we propose the adoption of sparse identification of nonlinear dynamical systems as an additional tool to distill closed-form expressions for the trained nets, that embed a more straightforward engineering interpretation. We demonstrate the framework on a series of numerical and experimental examples, with the latter pertaining to a structural system featuring highly nonlinear behavior, which is successfully learned by the proposed framework. The proposed structural identification with Physics-informed Neural ODEs comes with the benefits of direct approximation of the governing dynamics, and a versatile and flexible framework for discrepancy modeling in structural identification problems.

external page original source on JSV