An approach to Robust Damage Detection

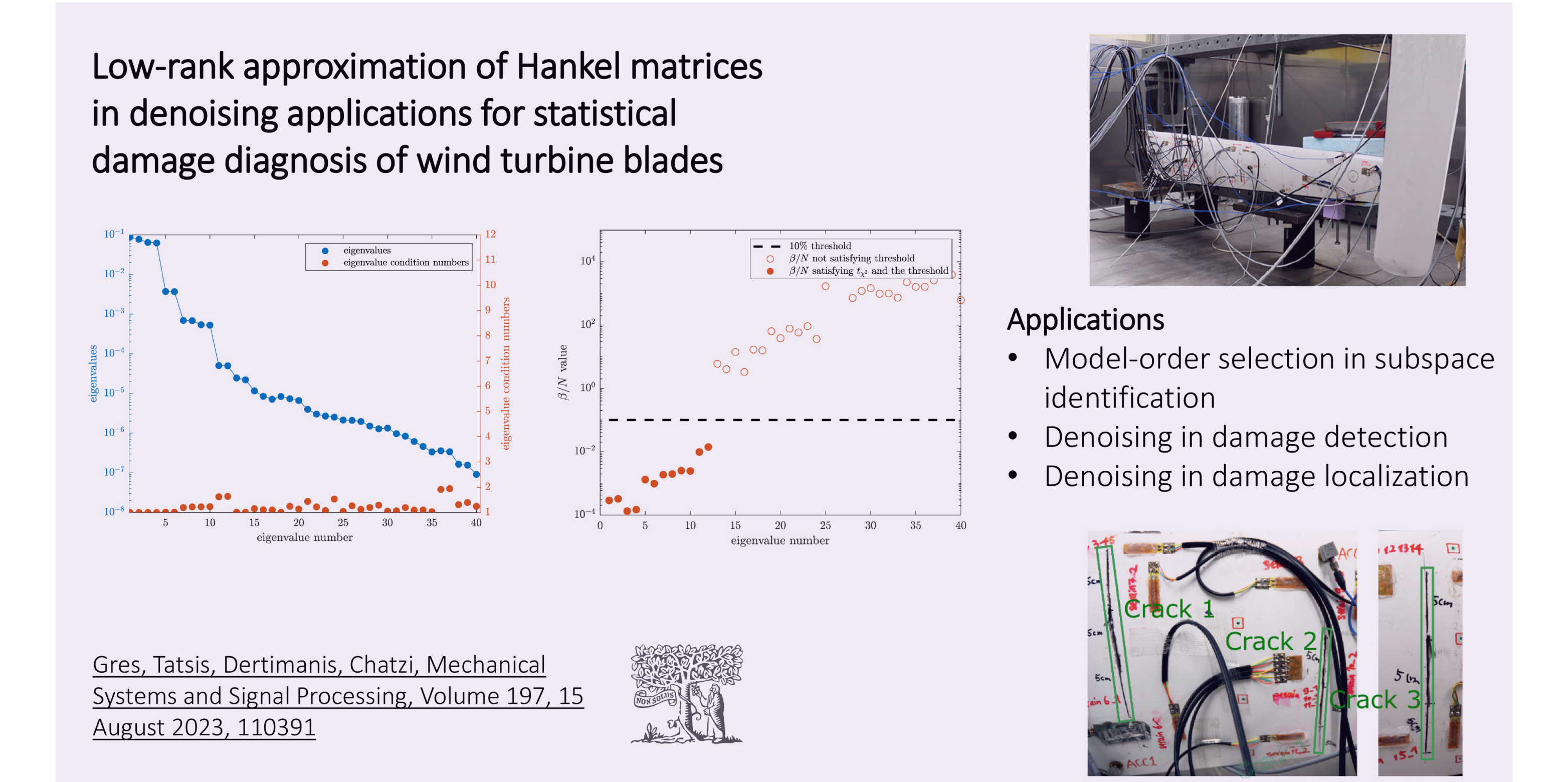
In this work, led by Szymon Gres, DFF Postdoc Fellow, we propose a method to actively select the low-rank structure of large output-only data-covariance Hankel matrices based on the statistical properties of its eigenvalue condition numbers. We apply it to reduce the number of false alarms and to enhance the detectability of small damages in data-driven damage detection of linear time-invariant dynamic systems; both, in the context of structural health monitoring of wind turbine blades.

The work delivers a number of theoretical insights; we show that the asymptotic distribution of the eigenvalue condition numbers of data-covariance matrices follows a dual framework, depending on the covariance of inputs acting on the monitored linear time-invariant system. For inputs whose covariance is proportional to the mass matrix, the asymptotic distribution of the eigenvalue condition numbers is approximated by a χ2 distribution. For inputs whose covariance is a random positive matrix, the condition numbers follow a Gaussian distribution. For both approximation frameworks, we devise an algorithm to distinguish the spurious eigenvalues from the remaining system eigenvalues, which is then applied to denoise the underlying data-covariance matrix.

This work has been carried out by the SMM team members: Szymon Gres, Konstantinos Tatsis, Vasilis Dertimanis, and Eleni Chatzi and was financed by the Independent Research Fund Denmark within the 'Fault quantification in operating wind turbines' project.

Read more about it in external page Volume 197 of MSSP.